Whosecoin Cryptocurrency

tl;dr

I helped design a secure proof-of-stake cryptocurrency using VRFs. Below, I detail the project as written in our paper.

Introduction

There is no doubt that Bitcoin uses a lot of energy. According to estimates by the Cambridge Center for Alternative Finance, the Bitcoin network currently uses 133 TWh of energy per year to support the mining process: approximately the same amount as all of Sweden. A single Bitcoin transaction uses 707.6 KWh of energy. There is a currently a high-profile debate as to the extent of Bitcoin’s current and future role in climate change. The exact breakdown of energy sources used in Bitcoin mining is unknown, but there is evidence that a sizable portion of the network still uses coal as their primary energy source. A large flood in a coal mine in Xinjiang, China over April 17-18, 2021 coincided with a full 1/3 reduction in the Bitcoin network’s computing power. If the reliance on fossil fuels continues, Bitcoin will be a large unnecessary contributor to global carbon emissions.

In direct contrast, proponents of Bitcoin argue that the Bitcoin network is a useful tool to accelerate global adoption of renewable energy sources necessary to halt climate change. Since renewable energy sources produce volatile energy output that fluctuates with the weather, they must be built far above capacity. Additionally, the best locations for building renewable energy farms are often in remote areas with little demand to justify the cost of construction. Bitcoin miners act as unique energy buyers that buy cheap energy during output peaks. In this manner, Bitcoin could be used as an economic battery to accelerate construction of renewable energy farms. Regardless of the possible merits justifying its high energy usage, Bitcoin alone is an unjustifiably slow and inefficient solution for high throughout DeFi and NFT applications. Alternative consensus mechanisms must be used as part of Layer 2 side-chain solution in order to scale PoW cryptocurrencies efficiently.

Bitcoin has not always used so much energy. According to the CCAF, Bitcoin only used around 6.7 TWh per year as late as 2017. Speculative investment in Bitcoin has caused its price to exponentially increase. Since the block reward rate is not tied to the market price of Bitcoin, large jumps in the Bitcoin price increase the profitability of mining Bitcoin and incentivizes more miners to join the network. Since Bitcoin rewards miners with Bitcoin roughly in proportion to their energy usage, one might expect Bitcoin energy usage to strictly increase if the price of Bitcoin rises. However, the Bitcoin block reward rate paid to miners is cut in half approximately once every four years. As long as the Bitcoin price does not continue to double more frequently than every four years, energy usage is expected to level out or even decrease. However, if the Bitcoin price continues to rise at a rapid rate, energy usage could increase further in the short term. Bitcoin miners receive a small fee from all transactions included in their block. Once the block reward has decreased to zero, transaction fees will be the sole source of revenue for miners. In order for the Bitcoin system to remain usable, there is a theoretical upper cap on the real world value of a transaction fee. Since the maximum number of transactions per block is fixed, there is a theoretical upper limit on the Bitcoin mining revenue. This also enforces an theoretical upper limit on energy usage in the long term.

In our paper, we define a PoS cryptocurrency that uses VRF based leader selection protocol in tandem with the Ten- dermint BFT finality gadget. Unlike other notable solutions which use a threshold-based VRF leader selection protocol which may elect multiple leaders or none at all, we define a network protocol which forms consensus on the global minimum VRF across the entire network. This approach makes the network extremely resilient to DoS attacks since the leader is not known by any node—including the leader—prior to consensus. Additionally, we create a REST API that node operators may optionally host which allows users to view the blockchain state using a React blockchain explorer frontend hosted on Github pages.

Background

Cryptocurrencies are built on top of unstructured peer-to-peer networks commonly known as gossip networks. In a gossip network, each node is connected to a small set of other nodes. Upon receiving a message, each node forwards the message to each of its peers. As long as the network is fully connected, any message broadcasted by any node should eventually reach every other node in the network unaltered. However, if malicious nodes are present in the network, this may not necessarily be the case. A malicious node in the network may arbitrarily choose not to forward messages. As long as removing all malicious nodes from the network does not partition the non-malicious nodes into two disconnected components, this does not prevent a message from reaching all nodes in the network. A malicious node in the network may attempt to alter the contents of a message. This can be prevented using cryptographic signatures. If a node signs a message before broadcasting it to the network, then all other nodes can verify that the message has not been altered before propagating it further.

Low-risk distributed protocols often make timing assumptions about the network to simplify application logic. For instance, web browsers have a preset timeout for HTTP requests after which they assume a response will never arrive. Since latency between nodes on a gossip network may vary wildly and security is of the utmost important to a cryptocurrency, it is important to understand and fully consider any timing assumptions made by cryptocurrency systems. In a synchronous network, we assume that all messages will arrive within some known upper time bound. This assumption is often made for distributed systems with lower security standards since it greatly simplifies analysis. For a high stakes application like a cryptocurrency, this is a dangerous assumption to make, since even a single message arriving outside of the latency upper bound can affect the security of the system. In an asynchronous network, we assume that all messages will eventually arrive, but there is no time bound on the message delay. Systems designed for an asynchronous network are more secure at the cost of complexity. The FLP impossibility result proved that it is impossible for a asynchronous distributed system to achieve deterministic consensus in the event that a single node malfunctions. Probabilistic algorithms, such as HBBFT or DUMBO achieve consensus in an asynchronous setting with overwhelming probability at the cost of complexity. In a semi-synchronous network, we assume that messages delay follows a probability distribution such that for any $\epsilon \in (0,1]$ , there exists a $\Delta t$ such that the probability that a message have a latency greater than $\Delta t$ is less than $\epsilon$ . The semi-synchronous network assumption is a convenient middle ground that is much more realistic than a synchronous network assumption, yet far more practical than asynchronous network assumptions.

The foundation of all prominent cryptocurrencies is a distributed database—often referred to as the ledger—that maintains the balance of all account holders. Unlike other distributed databases, cryptocurrency networks satisfy the following important properties:

Immutable History: Once a transaction is added to the database, it cannot be modified or removed. The entire history of transactions can be viewed and audited like a traditional financial ledger.
Byzantine Fault Tolerance: If any well-behaved node adds a transaction to their local copy of the database, then all well-behaved nodes will eventually add the same transaction to their database.
Nash Equilibrium: Nodes are fairly incentivized to operate in a correct manner as dictated by the network specification. Deviation from correct behavior should strictly hurt nodes.

In order to achieve the immutable history property, a cryptocurrency network structures the database as a blockchain. A blockchain is a linked-list of blocks in which each block references the previous block by its cryptographic hash. Each block contains a set of transactions that modify the database state at the previous block. In this manner, a blockchain implicitly stores the database state at every point in time. To modify the database state, a leader is chosen to propose the next block. Since a blockchain is intended to be an immutable ledger, it is important for nodes in the system to eventually achieve consensus on the state of the system. A block $b$ at height $h$ is finalized when it is common knowledge that all well-behaved nodes in the system agree that $b$ is the unique valid block at height $h$ . Bitcoin and Tezos achieves probabilistic finality in that the probability of a block being finalized approaches 1 as more blocks are added. Algorand uses a byzantine-agreement algorithm to achieve deterministic finality in that consensus is reached as soon as a block is added to the blockchain.

In a proof-of-work system, each node competes to be the first to create a block with a hash that is less than some constant value and broadcast it to the rest of the network. The probability of each node being the first to solve the problem is directly proportional to the speed at which they can compute cryptographic hashes. Each node independently considers the current state of the database to be defined by the longest correct chain of blocks and the leader of each round to be the first node to solve the problem for a block that adds onto the longest correct chain of blocks. A Nash equilibrium is incentivized by rewarding the leader by increasing their account balance. In this fully asynchronous model, two or more nodes may solve the hashing problem at approximately the same time, and the network may disagree on the current state of the database, so the network only reaches consensus with high probability after a sufficient number of blocks are added to the network.

In a proof-of-stake cryptocurrency, a Nash equilibrium is incentivized by rewarding nodes in proportion to their stake (account balance) in the network similar to an interest rate. Nodes that do not correctly participate may not receive a reward or even be penalized by with a decreased account balance. Similarly, nodes collectively vote in proportion to their stake, which prevent sybil attacks. A large real-world investment is required to gain significant control over the network. There are a wide variety of block proposal (leader selection) and consensus mechanisms in use by proof-of-stake cryptocurrencies.

Popular cryptocurrencies such as Binance Coin (BNB) using the tendermint-core blockchain utilize a weighted round-robin leader election protocol in order to decide which node should propose a block each round. The round-robin process cycles through all nodes in a pre-determined way such that each node is chosen to be leader in proportion to their relative stake in the network. This process uniquely selects a single leader for each round, but also allows a DoS attack to be efficiently executed since the leader of each round is known far in advance. A better theoretical model for blockchain leader election is the single secret random leader election (SSRE). A SSRE is a distributed process in which exactly one node is chosen to be leader. The election is random in that nodes are randomly chosen according to some predetermined distribution. The election is secret in that only the leader knows that they are chosen, but the leader can provide a proof to other nodes that they were chosen.

A verifiable random function $F: \{0, 1\}^{a} \to \{0, 1\}^{b}$ has an associated a set of functions $\text{(Gen, Prove, Ver)}$ such that $\text{Gen}(R) = (PK, SK)$ generates a public-secret key pair, $\text{Prove}_{SK}(x) = (y = F_{SK}(x), \pi_{SK}(x))$ generates a number $y$ and proof $\pi$ such that $\text{Ver}_{PK}(x, y, \pi) = 1$ if and only if $y = F_{SK}(x)$ . Importantly, the output of $F$ must also be indifferentiable from the uniform distribution. It is important to note that a VRF satisfies all the properties of a cryptographic signature with the additional requirements of uniqueness and uniform randomness. The VRF was first invented by Algorand founder Silvio Micali.

There are a couple of notable solutions that utilize the VRF to construct a random leader election. The Blind Assignment for Blockchain Extension (BABE) protocol uses a VRF threshold method to elect all nodes whose VRF for a round is less than a predetermined constant. This process may elect multiple leaders or may elect no leaders at all. A byzantine agreement can later be used to arbitrarily choose a single block from the set of potential blocks proposed by the leaders The Algorand protocol uses a VRF threshold method to select small committees from the full set of nodes. Each node in the committee proposes a block and the committee runs a byzantine agreement to determine the minimum VRF among all nodes in the committee.

A byzantine agreement is a distributed protocol used to achieve consensus among nodes where some fraction $f$ of the nodes may be faulty or even malicious. A malicious node may send an incorrect network message, send a network message at the wrong time, or fail to send a message at all. More formally, every byzantine agreement must satisfy two important properties. A byzantine agreement satisfies the safety property if the protocol guarantees that if any non-faulty node decides upon some value $v$ , then all non-faulty nodes will eventually decide upon the same value v given that $f < k$ . A byzantine agreement satisfies the liveness property if the protocol guarantees that some non-faulty node will eventually decide upon some value $v$ given that $f < k$ . Below, we detail the popular Tendermint byzantine agreement and provide a proof of safety. The Tendermint byzantine agreement makes semi-synchronous network assumptions. Although we do not currently use it in our implementation, this protocol could be used to guarantee both safety and liveness in our cryptocurrency.

t = 60;
R = 1;
B = createBlock(...);
I = 0;
L = false;

while (true) {
  broadcast (propose, H, R, B);
  while (T * R seconds have not elapsed) {
    upon receiving (propose, H', R', B');
    if (I = 0 and L = false and H = H' and R = R' and L = L' and priority(B) > priority(B')) {
      B = B'
    }
    else if (I != 0 and B contains proof of +2/3 prevote at round I(B') > I) {
      B = B';
      I = I(B');
    }
  }
  broadcast (prevote, H, R, B);
  while (T * R seconds have not elapsed or no +2/3 prevote with (H, R)) {
    upon receiving vote = (prevote, H', R', B') add vote to list;
  }
  if (+2/3 prevote B) {
    L = true;
    broadcast (precommit, H, R, B)
  }
  else if (+2/3 prevote B') {
    L = false;
    broadcast (precommit, H, R, null)
  }
  else {
    broadcast (precommit, H, R, null)
  }
  while (T * R) seconds have no elapsed or no +2/3 precommit with (H, R)) {
    upon receiving vote = (precommit, H', R', B') add vote to list;
  }
  if (+2/3 precommit B) {
    broadcast (commit, H, R, B)
  }
  else {
    broadcast (commit, H, R, null)
  }
}

We will prove that this protocol satisfies the safety property: if any node decides upon a block, all correct nodes will eventually decide upon the same block. If less than 1/3 of the nodes are faulty and a correct node receives a +2/3 majority $\text{Prevote}$ , then it knows that +1/2 of the correct nodes have the same block. If that same node then receives a +2/3 majority $\text{Precommit}$ , then it knows that +1/2 of the correct nodes have the same block and also know that they have the same block. Since a correct node locks in a block when they know that +1/2 of the correct nodes have the same block, the node also knows that +1/2 of the correct nodes have locked in to $B$ . A correct node will only unlock when they know that +1/2 of the correct nodes have a different block from them. This will never happen since +1/2 of the correct nodes are locked. A correct node will only commit a block if this is true.

If any correct node commits a block $B$ , then some set of +1/2 of the correct nodes must have either already committed $B$ or be currently locked on $B$ . In a fully asynchronous network, there is no guarantee that +1/2 correct nodes locked on $B$ will be able to communicate with each other. However, if we instead assume a semi-synchronous network, the probability that each of the +1/2 correct nodes will receive the $\text{Prevote}$ and $\text{Commit } B$ messages from the rest of the +1/2 correct nodes approaches 1 as $R \rightarrow \infty$ . Once the +1/2 correct nodes commit their blocks and broadcast a $\text{Commit } B$ message, the rest of the nodes will eventually receive +1/2 $\text{Commit } B$ messages and $\text{Commit } B$ the block themselves.

Our System

We model our system as an infinite repeating game of random leader elections, in which a fixed set of $n$ agents compete to generate the smallest random number. We then propose protocols for an iterated random leader election, security during volatile player sets, construction of a blockchain using the election process, and minor modifications resulting in a weighted proof-of-stake system.

At each time step $t$ , we seek to elect a random leader among all agents (this leader will add the next block to the chain). At a base level, the election process should be both random (election parameters are not easily manipulatable) and equitable (each agent has the same chance of being elected). We propose the following election process and defend it against the bolded criteria. Initially, all agents $i$ generate a random number $R_i$ and a public-private key pair $\text{GEN}(R_i) = (PK_i, SK_i) B$ . Agents know $PK_i$ for all other agents, but have no knowledge of $R_i$ or other $SK_i$ . During each round $k$ with random seed $T_k$ , all agents compute and publish their random number and proof defined below:

(y_i, \pi_i) = F_{SK_i}(T_k)

The winner of the round is the agent with the smallest $y_i$ such that $\text{VER}_{PK_i}(T_k, y_i, \pi_i) = 1$ . In other words, each agent generates a random number using the VRF and broadcasts it to the network. The elected agent is the one with the smallest verified $y_i$ .

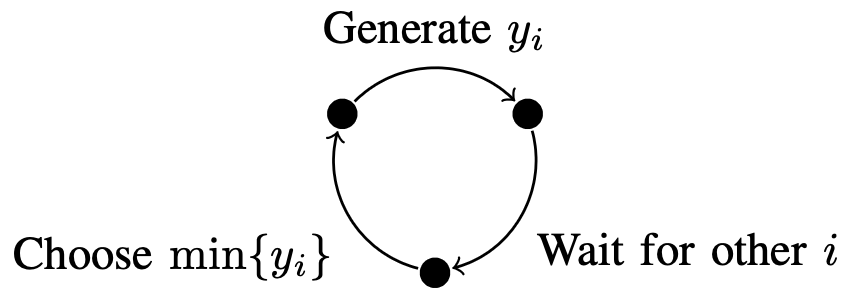
Assuming the VRF works as assumed, we see that this method is both random and equitable by construction. The random number assigned to each agent depends only on their secret key and the current seed, where the secret key is chosen without their knowledge and the current seed becomes increasingly random with successive rounds (proof of this is shown later). Additionally, since each agent gets a singular random number, the likelihood of being elected does not vary between agents.

Once a leader has been randomly elected at round $k$ , we must then set up the seed for round $k+1$ in a secure manner. An easy way to accomplish this is by introducing some aspect of randomness in order to prevent the possibility of any malicious agents purposefully generating a seed of their choice. Thus, we propose the following simple scheme to generate a new random $T$ for each round and argue its security below:

T_{k+1} = H(T_k|PK_w)

Here $H$ is a random oracle and $w$ is the agent who won round $k$ . The use of $H$ introduces the aspect of main aspect of randomness. Additionally, the inclusion of both $T_k$ and $PK_w$ serves to supplement this with additional factors that are hard to determine for asymptotically large numbers of agents.

We will show that this method of election is secure by examining the asymptotic probability that any malicious agent can guarantee their odds of winning successive rounds. It is possible for an agent $i$ with prior knowledge of the initial seed $T_0$ to generate many different random numbers $R_i$ in order to minimize their value $F_{SK}(T_0)$ prior to entering the game. The probability of randomly picking a number $x_0 < \epsilon$ from the random distribution $U \in [0, 1]$ is $\epsilon$ . The expected count of random numbers $R$ that must be generated before this bound is reached is $1/\epsilon$ . Assuming that generating a value less than $\epsilon$ is sufficient to guarantee a win with high enough probability, agent $i$ can guess $T_1 = H(T_0|PK_i)$ with high probability. The likelihood of winning for the first $k$ rounds of the game is $\epsilon^k$ , which requires an expected $1/\epsilon^k$ tries.

To ensure a win for $k$ cumulative rounds with probability $p$ , agent $i$ must win each round with probability $p^{1/k}$ . For some $\epsilon$ , if all other agents are non-malicious and pick truly random numbers, the probability of winning a given round is $(1-\epsilon)^n$ . Thus, the agent would need to choose $\epsilon = 1 - p^{1/kn}$ . Doing so would require an expected $1/(1 - p^{1/kn})^k$ attempts with random seeds. Even for small values of $k$ and $n$ , this value quickly approaches infinite. For example, a game with 10 agents would require malicious agent $i$ to attempt $7.54 \cdot 10^{32}$ seeds in order to find one ensuring election for 10 rounds with probability 0.95.

It is important to note that as soon as agent $i$ enters the game, they have no way to chance their random number. As soon as they lose a round, they lose all benefit from preemptively computing many different values of $R$ . However, this is not necessarily the case if we allow agents to enter and exit the game at will. If this were the case, any agent could perform a brute-force optimization to force their election in the game at any time (albeit for a small number of rounds limited by their computational resources as shown above). Assuming all agents act independently, this can be remedied by forcing all new agents to declare their public key at least two rounds before they start playing.

Dropping the assumption that agents act independently, a coalition of agents could collectively win for an arbitrary number of rounds in the following manner. Before the game starts, $a_0$ could pre-compute their seed to force a win on rounds 0 to 2. During round 0, $a_0$ could tell $a_1$ what $T_3$ will be and $a_1$ could pre-compute their seed to win rounds 3 and 4, then join the game during round 1 in time to play round 3. During rounds 1 and 2, $a_1$ could tell $a_2$ what $T_5$ will be, and the process continues. In this manner, as long as the agents can collectively pre-compute seeds faster than the game runs, their coalition can collectively dominate the game.

It is easier for a coalition to force a win over an arbitrary number of rounds because each agent only needs to compute a seed that forces a win over 2 rounds: a significantly easier problem. This problem can be remedied by forcing all agents to declare their public key further in advance. The amount of work per agent to perform a chained coalition attack increases exponentially with the number of rounds that an agent must join. Depending on the initial number of players and the expected payoff of winning a round, this value can be fixed so that it is computationally and economically infeasible for a chained coalition attack to occur.

We use the iterated random leader election above to build a blockchain in the following manner: when broadcasting a VRF proof for each round of the iterated election process, each node also proposes the next block in the blockchain. After receiving a VRF proof from each node, the block associated with the minimum VRF is committed to the blockchain. The benefit of this approach is that it is quite simple. However, a malicious node may create a fork in the system by proposing multiple blocks with the same VRF for each round. This vulnerability can be resolved easily by requiring all nodes to store the set of blocks associated with the VRF for each round. When proposing a block, each node must choose exactly one fork to build upon. Thus, as long as at least one well-behaved node is eventually elected leader, all forks will eventually be resolved. We characterize this property as eventually fork-free. After adding a Blockchain construct into the leader election protocol, in the absence of malicious nodes that propose multiple blocks when elected, each node knows the account balance of every other at every stage of the game. In presence of malicious nodes, each node knows the account balance of every other node with high probability after enough rounds have passed.

The fairness property of the leader election proposed above is conditional on the assumption that each agent can only create a single node. This is an unrealistic assumption, a single agent can win more elections by creating more nodes each with their own unique keypairs. To prevent this, we modify the iterated leader election protocol to randomly select each node with a probability equal to the node’s account balance divided by the sum of the account balance of all nodes in the network. Under this construction, a proof-of-stake cryptocurrency is fair if the expected reward at each round of the leader election is proportional to wealth at the previous round. We propose a modification to the initial iterated leader selection protocol that is approximately fair. For round $k$ with random seed $T_k$ and scaling factor $S$ , we assign each node with balance $W_k$ a priority $y_i$ .

(y_i, \pi_i) = \min_{n=1,\ldots, \lfloor W_k / S \rfloor}\{(y_n = F_{SK}(T_k + n), \pi_n)\}

The scaling factor $S$ is chosen based on the maximum total supply in order to limit the computational complexity of choosing the minimum priority at each round. When $S=1$ this is a fair random election. An unfortunate side effect of scaling the votes is that probability of winning the election is not exactly equal to network stake since the proposed function can only be run in integer values. We choose to floor rather than ceil this value to prevent sybil attacks: otherwise a node could drastically increase their probability of winning the random election by splitting their stake into many nodes with small stake.

This protocol satisfies the safety property: if any node decides upon the leader of the random election during any round, then all nodes will eventually decide upon the same leader of the election for that round. This protocol does not satisfy the liveness property: a single node, if they fail to send their VRF proof, can stall the network state indefinitely. We can utilize the Tendermint byzantine agreement to enforce liveness while maintaining network safety as long as less than 1/3 of the nodes are faulty.

Implementation

To represent objects on the network, we use a simple binary format based on the BSON specification. Unlike BSON, it does not have the capability to store key-value pairs. This allows us to send tuples of any type across the network. The benefit of using this format over a common format like JSON is that messages can be serialized and deserialized far faster than using JSON. The benefit of using this format over a simple binary representation such as that used by the Bitcoin protocol is that nodes can determine the type of a tuple that it does not understand or expect. This allows for easier error handling.

tuple   ::= "(" e_list ")"

e_list  ::= element e_list
          | ""

element ::= tuple // nested tuple
          | "i" int32_t  // big-endian 32-bit signed integer
          | "I" int64_t  // big-endian 64-bit signed integer
          | "u" uint32_t // big-endian 32-bit unsigned integer
          | "U" uint64_t // big-endian 64-bit unsigned integer
          | "f" float    // IEEE 754 single-precison float
          | "F" double   // IEEE 754 double-precison float
          | "b" bool     // 0x01 if true and 0x00 if false
          | "B" buffer   // arbitrary binary data
          | "s" string   // 0x00 terminated string
          | "n"          // null

buffer ::= uint32_t uint8_t[]

All network messages are composed of a message header and a message body. The message header contains a magic number which can be used to locate the start of a message in case a malformed message is sent, a domain specific integer representing the message "type," the length of the message body, and a random GUID unique to the message. The body of all network messages are binary tuples.

magic   ::= "0x54524a54"
guid    ::= uint32_t uint32_t uint32_t uint32_t
type    ::= uint32_t
length  ::= uint32_t
header  ::= magic guid type length
message ::= header tuple

There are two classes of messages on the Whosecoin network: direct messages and broadcasted messages. A direct message has a null guid. Any node which recieves a direct messages should act on the message, but need not forward the message to any other nodes. A broadcasted message has a non-null guid. Any node which receives a broadcasted message should forward the message to all of its peers unless it has already received a message with the same guid. Under this current system, a malicious node can prevent a message from reaching all nodes by modifying the message before forwarding it to its peers. If the incorrect message reaches a node before the correct message, the node will only act upon and forward the incorrect message. This can be resolved by including a message signature in the message header which can replace the GUID in this scheme.

We briefly highlight the network protocol message types below:

handshake: On connecting to the network, a node attempts to connect to all known peers.
peer-request: After connecting to a peer, a node requests a list of the peer’s peers.
peer-response: Upon receiving a list of a peer’s peers, a node attempts to connect to each one in turn.
block-request: A node requests all blocks starting with current leaf node of principal blockchain.
block-response: A node sends all blocks starting with the requested block.
pool-request: A node requests all transactions in a peers transaction pool.
pool-response: A node sends all transactions in their transaction pool.
transaction: After receiving a transaction, a node adds the transaction to a pool of unconfirmed transactions.
block: After receiving a block, a node adds the transaction to the blockchain database.

Shown below is the definitions for a block and a transaction in our code. The structs each have an equivalent typed tuple definition that is used to transmit them over the network.

struct block {
    uint64_t  timestamp;
    block_t  *prev_block;
    list_t   *transactions;
    uint8_t   merkle_root[crypto_generichash_BYTES];
    uint8_t   public_key[crypto_vrf_PUBLICKEYBYTES];
    uint8_t   signature[crypto_sign_BYTES];
    uint8_t   sortition_proof[crypto_vrf_PROOFBYTES];
    uint32_t  delegate;
}

struct transaction {
    uint8_t  sender[crypto_sign_PUBLICKEYBYTES];
    uint8_t  recipient[crypto_sign_PUBLICKEYBYTES];
    uint64_t value;
    uint32_t nonce;
}

Each node has the option to expose a simple REST API that allows users to query for the latest blocks on the blockchain, the current balance for any account. Shown below is the React front-end that was created to visualize the results of the blockchain explorer API.

Possible Extensions

In its current state, the system defined above exemplifies excellent security (malicious nodes cannot stop the system from moving from block to block) at the cost of poor liveness (nodes can potentially withhold blocks until later iterations and then roll back the system to a much earlier state). Due to time constraints, this was left unaddressed in the basic framework implemented above, but can be solved by implementing a fault tolerance system. Namely, we would seek to implement Byzantine fault tolerance using a similar system to Tendermint, which guarantees liveness (while maintaining safety) under the assumption that less than 1/3 of the nodes are malicious.

Additionally, the network currently operates through a shell, which is innately simple and might prove difficult for potential users to navigate. Should the network ever be implemented as a large-scale distribution, it would need to be adapted to include some kind of GUI. This was loosely done through the implementation of the blockchain explorer page, but additional steps can (and should) be taken to polish it up for real use.